
이번 포스트는 열역학 3법칙에 대해서 기술할 겁니다. 이제 이것을 마지막으로 열역학 파트가 끝나게 됩니다. 마지막 단원이라서 그런지, 간결하고 짧습니다.
Intro
먼저 절대 영도에 대해서 간략하게 언급을 해보겠습니다. 절대 영도는 인류가 절대 도달할 수 없는 온도입니다. 열역학적으로는, 모든 입자가 "바닥 상태"에 있는 온도이죠. 왜 도달하지 못할까요?

열역학 제2법칙에 대한 클라우지우스의 서술에 따르면, 일을 투입하지 않고 열이 반대로(고열원->저열원)으로 흐르게 하는 것은 불가능하다고 하였습니다. 그러면 충분히 많은 일을 해주면 계속 열의 흐름을 역으로 이용할 수 있을 것이고, 따라서 0K에 도달할 수 있지 않을까요?
먼저, 계의 엔트로피에 대해서 생각해봅시다. 지금껏 엔트로피를 많이 언급했지만, 이것을 어떻게 측정하고 구할 수 있는지에 대해서는 자세하게 언급한 적이 없습니다. 엔트로피는 물체의 열용량을 측정함으로써 구할 수 있습니다. 먼저 등압 열용량의 정의는

와 같습니다. 원래의 정의가 압력 p가 고정되어 있을 때 Q를 T로 미분해주는 것이었으므로, Q=TdS임을 이용하면 위와 같이 바꿀 수 있습니다.
여기서 양변을 T로 나누고, T에 대해서 적분해줌으로써 엔트로피 변화를 구해봅시다.

그러면 정적분의 정의에 따라 우변이 S(T)-S(T0)가 됨을 알 수 있습니다. 즉, 열역학 제3법칙은 T0=0K의 엔트로피에 대한 서술입니다. 제3법칙에 대한 서술은, 3가지의 경우가 있습니다. 과학자 3명이 각각 조금씩 다르게 서술을 하는데요, 이것에 대해 알아봅시다.
제3법칙의 여러 서술(different statements of 3rd law)
네른스트의 서술(Nernst's statement)
먼저 첫번째 서술입니다. 독일의 물리학자 네른스트(Nernst)의 서술입니다. 깁스 자유 에너지 G를 생각해봅시다. 깁스 자유 에너지는 엔탈피 H에서 온도 T와 엔트로피 S의 곱을 빼는 것으로 정의가 됩니다. 엔트로피가 변하는 과정이라면, 깁스 자유 에너지의 변화는 다음과 같이 표현됩니다.

여기서 T가 0에 가까운 계라고 가정하면, 당연히 TΔS의 기여가 0이 되어야 합니다. 그러면 오직 깁스 자유 에너지 ΔG는 엔탈피 변화 ΔH에 의해서만 결정됩니다. 따라서, ΔG는 ΔH에 수렴합니다.
이것은 당시 저온 물리 실험을 하던 네른스트가 실험적으로 확인한 결과입니다. 이걸 그래프로 나타내면, 위 사진에서 오른쪽 그림과 같이 나타나게 됩니다. 여기서 단순하게 접점으로만 수렴하는 것이 아니라, 기울기 자체도 0으로 수렴하는 것이 주목하여야 할 결과입니다. 이를 토대로, 네른스트는 열역학 제3법칙을 도입했습니다. 다음은 네른스트의 열역학 제3법칙입니다.

제가 설명했던 그래프를 조금 자세하게 생각해보면, 절대 영도에 가까워질수록 엔탈피 변화(엔탈피 기울기)가 0에 가까워집니다. 그러면 곧 깁스 자유 에너지 변화는 ΔS에 의해 결정되어야 합니다. 그리고 이 ΔS 역시도 깁스 자유 에너지의 기울기로써 나타나게 되겠죠. 그런데 엔탈피 H와 엔트로피 S, 둘 다 기울기가 0이 되는 모습을 보여주고 있으니, 이것은 엔트로피 변화가 없다는 소리가 됩니다!
임의의 과정(깁스 자유 에너지가 변하는)에 대해서, 절대 영도에 가깝기만 하면 엔트로피 변화 없이 일어날 수 있다는 것이죠.
플랑크의 서술(Plack's statement)
그리고 또 다른 물리학자, 플랑크(M. Planck)는 네른스트의 열역학 제3법칙을 조금 수정하였습니다.

플랑크는 열역학 제3법칙이 완벽한 결정 구조에서만 서술이 가능하다고 이야기하였지만, 실제로는 계와 상관없이 통용되는 것으로 추측됩니다. 조금 보완된 점은, 엔트로피 자체를 0으로 둘 수 있다고 확연하게 언급이 되어있다는 점입니다.
이 소리를 통계역학적으로 생각해봅시다. 우리가 지금까지 중간중간 언급했던, 통계역학적 엔트로피의 정의에 따르면 다음과 같습니다.

미시 상태의 수, microstate 수가 log 취해지므로 1이 되어야 엔트로피가 0인 상태가 됩니다. 하지만 실질적으로 우리가 계를 다루다 보면, 계가 여러 개의 바닥 상태를 가지거나 거의 바닥 상태에 가까운 경우가 있습니다. 즉, 정의에 따르면 엔트로피가 0은 아니지만 매우 작은 수인 경우죠.

따라서, 조금 더 일반적인 케이스까지 포괄하게 되면, "엔트로피는 절대 영도에서 유한한 값으로 수렴한다"가 정확한 표현이 되겠습니다.
사이먼의 서술(Simon's statement)
추가로 열역학 3법칙은 하나의 서술이 더 존재합니다. Simon에 따르면 다음과 같이 기술됩니다.

뭔소린지 이해가 잘 가지 않는다면, 첫번째 서술에서 언급한 깁스 자유 에너지의 변화량에 대해 집중하면 됩니다. ΔG=ΔH-TΔS입니다. 여기서 온도가 극한으로 낮아지게 되면(절대 영도에 가까워지면), 엔트로피 변화량의 기여도는 어차피 곱해져도 0이 되기 때문에 의미가 없어지게 되죠.
제3법칙에 대한 결론(consequences of the 3rd law)
이번에는 이렇게 언급한 3법칙을 통해 결론을 내봅시다. 만약, 다음과 같이 T가 0에 접근하는 과정이라면

열용량 C(등압/등적 열용량 모두 가능합니다)는 위와 같이 온도에 대한 엔트로피의 극한으로 표현할 수 있습니다. 이것은 도함수의 정의에 따라 각각 엔트로피와 온도의 증가량 비로 표현할 수 있습니다. 이 때, 열역학 제3법칙의 가정을 이용합니다(절대 영도에서는 엔트로피가 일정 값으로 수렴한다는 가정). 그러면, 결국 전체 극한값인 열용량 역시도 0에 수렴하는 것을 알 수 있습니다.
이 논의는, 다음과 같이 이어집니다. 아까 위에서 절대영도에 가까워질수록 엔트로피가 일정한 값으로 수렴하는 것을 보였습니다. 만약, 엔트로피가 압력에 의존하지 않는다면(압력에 대해 상수인 경우라고 생각하시면 됩니다), 엔트로피를 고정된 온도에 대해 압력으로 편미분한 값은 0이 됩니다.

여기서 맥스웰 관계를 적용합시다. 그러면, 위와 같이 부피를 고정된 압력에 대해 온도로 미분한 것과 같으며, 이것을 통해 붉은색 글씨로 표현된 열팽창 계수가 곧 0이 되어야 함을 확인할 수 있습니다. 따라서 절대영도에서 열팽창은 없습니다!
두번째 결론입니다. 이상기체의 열용량을 각각 3R/2, 5R/2로 구했었는데요, 이것은 온도에 무관한, 상수입니다. 그러나 위에서는 분명히 절대영도에서 열용량이 0이 된다고 이야기 했습니다.

즉, 이 소리는 이상기체가 실재할 수 없다는 것입니다.
마지막 결론입니다. 자성(magnetism)으로까지 확장해봅시다. 만약 엔트로피가 절대 영도에서 외부 자기장에 의존하지 않는다면,

위와 같은 논리를 통해 엔트로피 S를 자기장 B로 편미분한 값은 맥스웰 관계에 의해 자기 쌍극자 모멘트 m을 온도 T로 편미분한 값과 같으며, 이것은 자기 쌍극자의 정의에 따라 감수율(susceptibility) 꼴로 표현할 수 있습니다. 그런데 이때 0 K에서 온도에 대한 자기 감수율은 0이 되어야 합니다.

그런데 참 이상합니다. Curie-Weiss 법칙에 따르면 자기 감수율은 온도에 반비례한다고 했단 말이죠. 사실, 이것은 일반적으로 고온에서 잘 맞습니다. 실제로는 온도가 낮으면, 자기 쌍극자를 만들어내는 근원인 '스핀'이 정렬하게 됩니다. 물체의 성질(물성)에 따라 스핀의 정렬 방식이 조금씩 상이합니다(상자성, 강자성, 반자성, 반강자성 등). 이것은 결국 온도 변화에 따라서 자기장에 둔감해진다는 것을 보여줍니다.
그리고 우리는 저온 냉각 과정을 '스핀'의 정렬을 통해서 이어갔는데, 이것은 곧 물질의 스핀이 정렬되어 자기장에 둔감해짐에 따라, 절대 0도에 도달하기 어려워짐을 보여줍니다.

따라서, 유한한 과정을 거쳐서 절대 0도에 도달할 수 없습니다. 왜 굳이 유한한 과정이라고 언급하였을까요? 아래의 그림을 보면 조금 이해가 쉬울 겁니다. 완벽한 설명은 아니지만, 충분히 유용합니다.
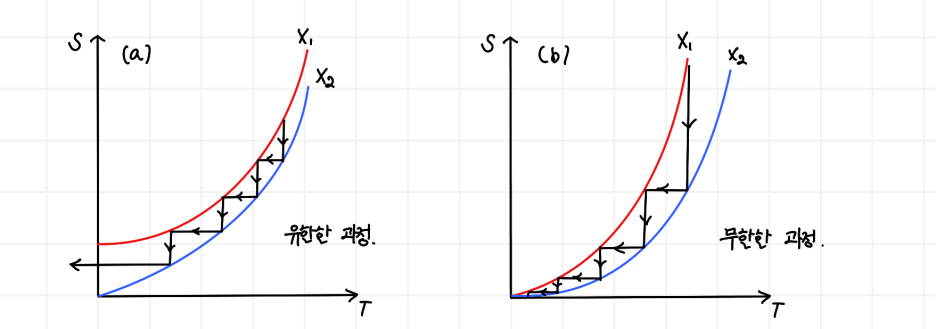
두 그림을 보면, 두 열역학 변수 X**1과 X2**(자기장이 될수도 있고, 다른 요소가 될수도 있습니다!)에 대한 엔트로피 감소 곡선의 개형이 조금 다릅니다. 만약 (a)와 같은 개형을 가진다면 우리는 유한한 과정을 통해서 결국 물질의 엔트로피를 일정 값으로 수렴시킬 수 있습니다. 그러나 실제로는 (b)의 개형을 가집니다. 이러한 경우 두 상태의 엔트로피 차이가 저온으로 갈수록 굉장히 작아집니다. 그러면 실질적으로 실행시켜야 할 열역학적 과정(화살표 수로 생각하시면 됩니다)이 무한하게 늘어나게 됩니다.
결국 자기 소거를 통한 냉각은 단열 과정과 등온 과정을 거치면서 온도를 낮추는 것인데, (a)의 경우는 열역학 제3법칙이 적용되지 않는 계이기 때문에 유한한 과정을 통해 도달할 수 있으나,

(b)의 경우 열역학 제3법칙이 '적용된' 계이고, 따라서 두 곡선이 최소 엔트로피 지점에서 만나므로 무한한 과정을 필연적으로 가져야함을 보여줍니다.
이렇게 18장이 끝났습니다. 비로소 열역학 파트가 마무리 되었네요. 이제부터 열 및 통계물리학 카테고리에 적혀질 이후의 포스트들은, 통계역학(statistical dynamics)을 중심으로 내용을 전개해 나갈 것입니다.
'물리학 > 열&통계물리학' 카테고리의 다른 글
| 20. 분배 함수(The Partition Function) (0) | 2024.08.24 |
|---|---|
| 19. 에너지 등분배(Equipartition of Energy) (0) | 2024.08.24 |
| 17. 막대, 거품, 자석(Rods, Bubbles, and Magnets) (2) | 2024.08.24 |
| 16. 열역학 퍼텐셜(The thermodynamics potential) (0) | 2024.08.24 |
| 15. 정보 이론(Information Theory) (0) | 2024.08.24 |