
아래의 내용을 이해하기 위해서는 통계역학적 개념이 필요합니다. 잘 이해가 가지 않는다면 제 블로그의 열/통계물리학 글을 읽고 오시길 추천드립니다.
$\text{Preface.}$
열물리학에서도 언급이 되었던 내용이지만, 이상 기체의 열용량은 통계물리학에서의 '등분배 정리'를 통해 유도할 수 있음을 보였습니다.

기체의 운동에너지가 3 방향으로의 자유도(degree of freedom)를 가지고 온도에 비례함을 확인할 수 있죠. 이것이 더 확장되어 대부분의 고체의 열용량의 경우는 3kB(원자 당)를 가진다는 것을 알고 있었습니다(실험적으로).

이것을 뒬롱-프티 법칙(Dulong-Petit Law)이라고 합니다. 그러나 법칙이라고 부르기엔 애매한 것이, 이 법칙이 항상 모든 고체에 대해 들어맞지는 않는다는 것입니다. 예를 들어 다이아몬드는 3R per mol을 만족하지 못하고 그것보다 작은 값을 가집니다. 또한, 온도가 변함에 따라 열용량이 달라지기도 합니다.

이것은 열용량이 온도 의존성을 가진다는 것을 의미합니다. 실제로 열용량은 저온 극한에서 급격히 감소하며(열역학 제3법칙), 반대로 고온에서는 증가하는 경향을 보입니다.
이것을 이론적으로 확인하기 위해 1896년, 볼츠만(Ludwig Boltzmann)은 원자와 원자 사이의 결합들이 만들어내는 조화 퍼텐셜(harmonic potential) 우물에 원자가 갇혀있다고 가정하고 이론적인 전개를 이어나갔습니다.

원자간 결합은 세 방향으로의 자유도를 가지고 있고, 등분배 정리에 따라서 3kB per atom의 열용량을 가지게 됩니다. 즉, 뒬롱-프티 법칙을 이론적으로 설명할 수 있었던 것입니다.
그러나, 위에서 언급했듯 저온에서는 이 법칙이 들어맞지 않았고, 아인슈타인(A. Einstein)은 이것에 의문을 가지고 더 정확한 이론을 기술하기 위해 새로운 가정을 도입했습니다.
1) 아인슈타인의 계산(Einstein's calculation)
기본적인 가정은 볼츠만의 가정과 비슷합니다. 원자들이 조화 퍼텐셜 우물에 갇혀있으나 모든 원자들의 진동수가 하나로 고정되어 있다고 가정하였습니다. 이때 이러한 진동수를 아인슈타인 진동수(Einstein frequency)라고 합니다.
우리는 조화 진동자(harmonic oscillator)에 대한 양자역학 문제를 이미 풀어서 그 해답을 알고 있습니다. 이러한 지식을 기반으로 조화 진동자의 열용량을 계산해봅시다.

1차원 단일 원자 진동자의 에너지 고유값은 위와 같이 구할 수 있습니다. 또한 통계역학에서 평균 에너지를 구하는 방법은 다음과 같고

여기서 i 상태의 에너지 Ei를 가질 확률인 Pi는, 볼츠만 인자(Boltzmann factor)에 비례합니다. 이때 사용된 기호인 β는 (1/k**B**T)로 정의된 값입니다.
그리고 우린 통계역학에서의 가장 기초가 되는 함수인 분배 함수(Partition function)을 구할 수 있습니다. 분배 함수의 정의는 볼츠만 인자의 sum으로 나타납니다. 그런데 우리는 위에서 1차원 운동에 관해서만 고려하였으므로 헷갈리지 않도록 분배함수에 아래 첨자로 1D를 써줍니다. 위에서 주어진 1차원 단순 조화 진동자의 에너지를 대입해주면

의 값을 구할 수 있습니다. 이때 사용된 테크닉은 별건 아니고, 기하급수 공식을 이용해서 계산한 뒤 hyperbolic function 형태로 정리한 것입니다.
자, 그리고 이제 분배 함수로부터 평균 에너지를 구할 수 있습니다. 결론적으로는 가장 위에서 언급했던 정의를 따라가는 것과 동일한데, 분배 함수의 로그값에 미분을 취하는 형태로써 위의 계산 과정을 한번에 진행할 수 있습니다. 이 내용은 통계역학 파트(분배 함수)의 포스트를 보시면 그 과정이 이해가 가실 겁니다.

그러면 coth 형태의 함수를 얻을 수 있고, 이것을 잘 정리하면 nB(보스-아인슈타인 분포함수; Bose-Einstein distribution)로도 표현할 수 있습니다.
이제 우리가 구하고자 하는 물리량인 열용량의 문턱까지 온 상황입니다. 열용량의 정의는 온도 변화에 따른 에너지 변화량이므로 평균 에너지를 온도로 편미분해줌으로써 구할 수 있습니다. 그러면 아래의 값을 얻고,
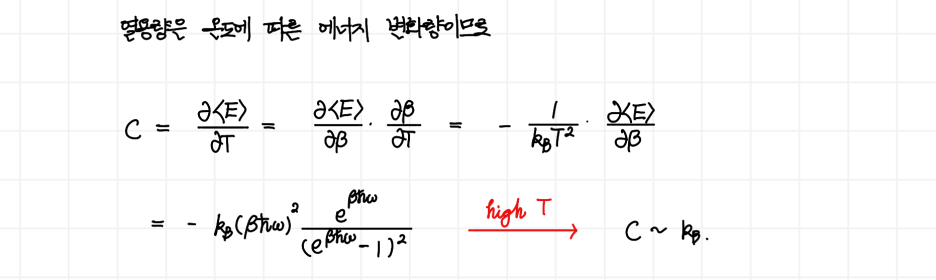
이것의 고온 극한을 취해보면 kB의 값을 얻을 수 있습니다. 극한을 취하기 조금 복잡한 상황인데, 이러한 경우 로피탈 정리를 사용하면 쉽게 확인할 수 있습니다. 이제 여기서 슬슬 감이 잡힐텐데, 우리는 지금까지 1차원 문제를 풀고 있었고 3차원 문제로 확장을 해야 할 필요가 있습니다. 따라서 3차원 공간에서의 조화 진동자 에너지는

이고, (1/2을 세 방향에 대해서 묶어서 3/2로 표현했습니다) 따라서 3차원 분배 함수는

지수에 있던 3이 계수로 빠지게 되면서(ln을 취했기 때문입니다) 1차원 문제와 정확히 3배만큼 차이나는 값을 얻을 수 있습니다. 위와 동일하게, 계수 뒤의 함수들은 동일하므로, 고온 극한과 저온 극한에서의 결과값을 살펴보면 다음과 같습니다.

고온 극한의 경우, 위에서 언급한 뒬롱-프티 법칙과 일치하나, 저온에서는 여전히 0으로 접근하게 됩니다. 이것은 저온에서 자유도(DOF)가 얼어붙기(freezing) 때문입니다.
그리고 아인슈타인 진동수를 열에너지와 비교하여 값을 도출하기 위해 아래와 같이 쓸 수 있습니다.

따라서, 이러한 아인슈타인의 모델은 고온에서는 적절하게 근사가 되지만 저온에서의 열용량이 0에 수렴하는 것을 설명하지 못하므로 한계가 존재합니다. 이것을 해결하기 위해 또 다른 물리학자가 등장합니다.
2) 디바이의 계산(Debye's calculation)
아인슈타인의 비열 이론은 굉장한 이론이었지만, 실제 값과 비교하여 명확한 오차가 존재합니다. 실제로 저온에서는 온도의 세제곱에 비례하는 열용량을 값을 얻게 되는데요,

이러한 문제를 1912년, 피터 디바이(Peter Debye)가 등장하여 해결합니다. 디바이는 원자 진동에서의 양자역학을 조금 더 매끄럽게 다루는 방법을 찾았으며, 비열의 T3 의존성을 설명하게 됩니다. 원자의 진동은 포논(phonon)이라는 입자로 해석할 수 있습니다. 디바이는 플랑크가 빛을 양자화했던 것처럼 진동을 양자화하였고, 여기서 빛과의 가장 큰 차이는 파동적인 성질에서 발생합니다.

빛, 즉 전자기파의 경우 진행 방향에 대하여 파동의 편광 방향은 수직합니다. 따라서 3차원 공간 상에서 두 가지의 mode가 존재할 수 있는데요, phonon의 편광 방향, 즉 k 벡터의 편광 방향은 3가지가 존재합니다(1개의 종파, 그리고 2개의 횡파).
문제를 풀기에 앞서 주기적 경계 조건(Periodic Boundary Condition)을 가정합니다. 이 논의는 열역학에서 자세하게 논의되어 있으니 참고하세요. 이러한 경계조건을 보른-폰 카르만(Born-Von Carman) 경계조건이라고 합니다.

r에서의 파동의 위상과 r+L에서의 파동의 위상이 같은 상태라고 가정하고 문제를 푸는 것입니다. 이러한 경계조건을 가질 때, k 값은 다음과 같은 조건으로만 존재할 수 있습니다.

여기서 사용한 문자 n은 정수(integer)를 의미합니다. 즉, k값은 이산적(discrete)입니다. 여기서 sample의 전체 길이 L이 매우 크다고 가정하면(고체의 길이 L에 비해 원자의 길이는 굉장히 짧겠죠?), 열역학적 극한(thermodynamic limit)으로 취급할 수 있어서 k값에 대한 sum을 integral로 치환할 수 있습니다.
이것은 1차원적인 논의에서 단순하게 가정한 것이고, 실제로는 k space 안에서 k 벡터는 세 가지 성분에 의해서 결정됩니다. 그 값이 n1 ~ n3라고 합시다.

따라서 3차원 공간으로 확장하면 적분은 다음과 같이 바뀌게 되며,

평균 에너지 역시도 위와 같이 바뀌게 됩니다.
여기서 디바이는 "고체의 진동 모드에 대해, 진동수가 파동의 속도와 파수 벡터 크기의 곱으로 나타난다"고 결론을 내렸습니다.

그리고 위의 식은, 아래에서 언급할 phonon의 상태 밀도 함수 g(ω)인데 이 상태밀도함수를 디바이 진동수 ωd까지 적분하게 되면 고체의 총 진동모드의 수 3N(N은 고체를 이루는 원자 수)를 가지게 됨을 의미합니다. 이것은 아래에서 디바이 진동수를 논할 때 이용합니다.
여기서 k 벡터가 구 대칭성(spherical symmetry)을 가지고 있으면(즉, 에너지가 파수벡터의 크기에만 의존하는 경우를 말합니다) k 값은 디바이의 가정에 따라 아래와 같이 표현되고

또한 k에 대한 적분을 1차원 적분으로 변환하여 마지막 항처럼 표현할 수 있습니다. 이제 k를 진동수 ω 형태로 치환하여 평균 에너지를 구하는 식에 대입해보겠습니다. 그러면,

을 얻을 수 있습니다. g(E)는 DOS(Density of State; 상태밀도 함수)를 의미하고, f(E)는 분포 함수(distribution function)를 의미합니다. 우리는 phonon에 대해서 다루고 있으므로 f(E)는 보스-아인슈타인 분포함수가 되겠네요. 이렇게 평균 에너지, 열용량 등의 물리량들을 구할 때 이러한 통계역학 공식은 많이 사용되므로 알아두면 정말 도움이 됩니다.
다시 돌아와서, 방금 언급했던 phonon의 상태 밀도 함수를 유도할 수 있고, 위에서 언급한 총 진동모드 수에 대한 조건을 이용하면 디바이 진동수(Debye frequency) 형태로 표현할 수 있습니다.
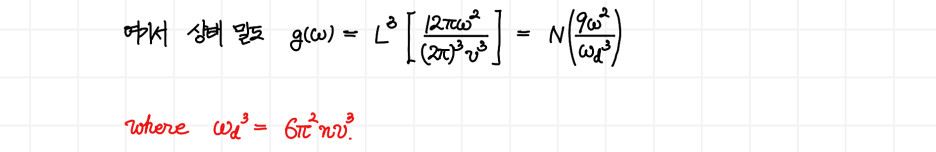
이 과정은 아래에서 자세하게 소개를 할터이니 일단은 넘어가도록 합시다. 이렇게 구해진 상태밀도 함수(DOS)를 곱해주고 적분을 취해주면 평균 에너지 를 구할 수 있습니다.
그리고 우리가 구하는 것은 열용량 C이므로 이것을 온도에 대해서 미분하여주면 열용량을 얻을 수 있습니다.

이제 약간의 (결과를 미리 알고 하는)테크닉인데, 피적분함수 중에서 (+1/2) 항이 보이시나요? 이 항은 어차피 미분하면 제거될 항입니다.

따라서, 지금부터 이 (+1/2)항을 무시하도록 하겠습니다. 그리고 미분이 아닌, 적분을 먼저 취하겠습니다.

피적분함수의 지수에 올라가 있는 βħω를 x로 치환해주게 되면 우변처럼 변하는데요, 이때, 새로이 나타난 피적분함수는 리만-제타 함수(Riemann-Zeta function)와 관련있는 값입니다.
이 적분을 보스 적분(Bose integral)이라고 하는데요, 제가 열/통계물리학 포스트에서 이 적분의 계산과정을 자세히 다루지 않은 것 같아(만약 중복되는 내용이면 댓글 남겨주세용!) 과정을 조금 설명해보려 합니다.
추가: 보스 적분(Bose Integral)
일단, 위의 경우에서는 x의 차수가 3인 경우이지만, 자주 등장하는 적분이기 때문에 일반화(generalize)시켜서 나타내 보겠습니다. 여기서는 n차항(n th order)인 경우입니다.

먼저 분모와 분자에 각각 exp(-x)를 곱해줍니다. 이때 xn을 제외한 분수 값은 등비급수(geometric series)의 극한 임을 쉽게 알 수 있습니다. 따라서 이것을 Sum 형태로 표현해줍시다. index는 k를 사용하였습니다(n과 혼동하지 않기 위해).
그리고, 소괄호 밖에 있는 exp(-x)를 괄호 안에 흡수시킨 뒤 급수를 조작합니다. 그러면

을 얻는데, 여기서 적분과 합의 index가 다르므로 연산 순서가 바뀔수 있습니다. 적분 연산을 먼저 취해줍시다. 그리고 약간의 치환을 하겠습니다. (k+1)x를 y 꼴로 표현할 것인데요.

그러면 결과적으로 아래와 같은 식을 얻게 됩니다.

놀랍게도 급수와 적분은 정확히 각각 제타 함수와 감마 함수로 나누어집니다.
신기하죠?
따라서 위의 결과를 이용하면, 평균 에너지 는 다음과 같이 구해집니다.

온도 네제곱에 비례하는 값입니다. 이것을 온도 T에 대해서 한 번 미분해주면 다음과 같이 3차항을 얻을 것이고

이것은 결국 온도의 세제곱(T**3)에 비례하는 열용량을 줍니다. 즉, **디바이의 계산이 저온에서의 열용량을 설명하게 된 것을 보여주죠.
부록: Density of State-g(ω) 구하기
이제 위에서 미루었던 g(ω) 함수를 구해보도록 하겠습니다. 사실 DOS를 구하기 위해서는 다른 방법도 이용할 수 있습니다. 운동량 공간(k-space)에서 점을 찍어서 구면 대칭성을 갖는 k 벡터에 대해 몇 개의 점이 존재할 수 있는지...하는 방법을 통해서 구할 수 있습니다. 하지만 그건 이제 귀찮아져버린 주인장입니다.
그것보다 조금 더 엄밀하고 일반적인 방법이 있어서 소개하겠습니다. 사실 열/통계물리학 포스트에서 이미 언급한 내용이지만 고체물리학에서 중요하게 다루어져서 저도 다시 한번 되새길 겸 작성해봤습니다.
먼저, 일반화된 DOS의 정의는 다음과 같이 델타 함수와 적분을 통해서 정의할 수 있습니다.

우리는 3차원 공간에서의 계산을 주로 다루므로 n = 3인 경우를 고려합니다(저차원 물리를 다루는 경우 n = 2 역시도 가능합니다! 저차원에서는 특수하게 작용할지도?).
그리고 수식에 에너지(ε)와 파수(k)를 다루고 있는데 이 둘 사이의 상관관계를 나타내는 분산 관계(dispersion relation)을 구하여야 합니다. 고체물리에서는 주로 phonon을 다루고 있고, Debye의 가정대로 선형 관계를 고려합니다.
또한, 빛과 가장 크게 다른 점 중 하나인데 phonon은 편광(polarization) 자유도가 3입니다. 따라서 상태수에 3을 곱해주어야 합니다.
자, 이제 준비가 되었습니다. k에 대한 함수로 바로 유도할 수 있겠지만, 에너지로 다루는 것이 기본적이기 때문에 먼저 g(ε)를 풀어써줍니다. k의 3차원 적분을 1차원 적분으로 다운그레이드합니다. 그러면 4πk2이 계수로 나오게 되죠.

그리고 디랙 델타 함수의 성질에 따라 아래와 같이 풀어쓸 수 있고(에너지를 k로 미분해주어야 합니다),

따라서 에너지에 대한 DOS를 구할 수 있습니다.

이렇게 되면 완성된거나 마찬가지입니다. 식 조작을 거치면 원하는 어떤 형태로든 이용할 수 있습니다. 책에서는 에너지가 아니라 각진동수 ω로 다루니까, g(ω) 형태로 바꾸어 보겠습니다. 이때 유의하여야 할 점은, g(ε)=g(ω) 형태로 바로 치환할 것이 아니라, g(ε)dε=g(ω)dω의 등식을 이용하여 바꾸어 주어야 한다는 것입니다. 자주 실수하는 부분이니 조심하세요.
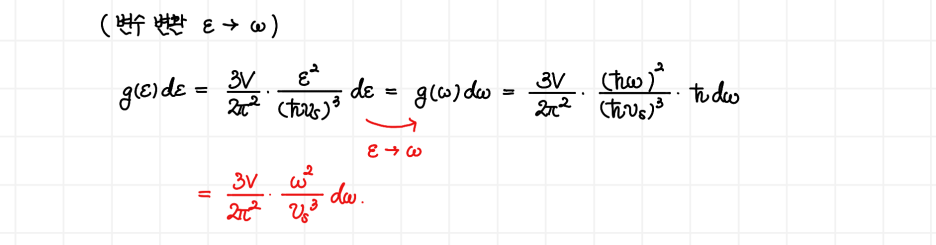
이제 디바이가 high frequency에서의 g(ω) 점유율이 낮다고 가정하고 도입한 cutoff frequency(Debye frequency)를 이용합니다. 아래의 식은 DOS의 정의를 나타낸 것으로, 전체 상태밀도를 모두 적분하면 총 자유도인 3N이 되어야함을 이용했습니다.

이렇게 Debye frequency를 얻었습니다. 번역본(3판 기준)에는 디바이 진동수(ω**D**)의 차수가 2로 나와있는데, 이것은 잘못된 것입니다. 3이 맞습니다. n은 밀도로, 입자 수를 부피로 나눈 값입니다. 이 결과를 이용하여 다시 g(ω)를 표현하면,

을 얻습니다.
이제 2장이 마무리 지어지고 있습니다. 이제 극한에서의 Debye model 열용량을 알아봅시다. 계산은 다 되었는데, 정말 우리가 알고 있는 사실과 일치하는지 확인해봐야겠죠?
평균 에너지를 다시 쓰면

을 얻었습니다. 이때 저온의 경우, 4차항을 미분하였으므로 3차항이 되어

온도의 세제곱에 비례하는 열용량을 얻었습니다(아인슈타인이 설명하지 못했던 부분).
그리고 고온에서는 어떨까요? 과정이 꽤 복잡하지만 천천히 가봅시다. 먼저 T가 무한히 크다고 가정하면, (1/kBT)로 정의되는 β값은 0에 수렴하게 됩니다. 위에서 평균에너지 적분식을 다시 한 번 살펴보면 피적분함수가 exp(βħω)꼴로 표현되는데요. 이것을 series 형태로 표현하겠습니다.

exp의 Taylor series 형태를 사용합니다. 분모에다 위 표현을 대입해주면

상수항은 지워져서 사라지게 됩니다. 이때, β→0인 경우를 가정하였으므로 가장 dominant하게 작용하는 항은 당연히 1차항(1st order) 입니다. 따라서 나머지 항을 무시하면

을 얻습니다. 즉, 고온 극한에서 (k**B**T/ħω)를 보스-아인슈타인 분포 함수(distribution function f(ω))로 사용할 수 있다는 것입니다! 적분하기 골치 아팠던 친구를 상수로 바꿀 수 있는 기회가 마련되었습니다. 이 표현을 대입해서 평균 에너지를 구해봅시다. 그러면 공교롭게도 ħω가 상쇄되며 사라지고

상태밀도함수 g(ω)의 정의에 따라 3Nk**B**T의 평균 에너지를 얻습니다. 이것을 T에 대해 미분해주면

C=3Nk**B** 의 열용량을 얻습니다(뒬롱-프티 법칙). 즉, 실험적 결과와 일치합니다!
요약 및 Debye model의 한계
그러나 Debye model이 완벽하다는 것은 아닙니다. 일단 첫번째로

Debye가 도입한 cutoff frequency는 ad hoc(즉흥적)입니다. 무언가에 의한 인과관계로써 설명되는 것이 아니라 계산 결과를 맞추기 위해 즉석에서 도입한 것이라는거죠. 후술하겠지만 이것에 의한 문제점이 충분히 존재합니다.
또한, 각진동수 ω와 파수 k 간의 선형 분산 관계는 고온에서 어긋나는 조건입니다!

그리고 실제 DOS는 우리가 구했던 형태와 다르며, 실제 고체의 열용량을 자세히 살펴보면(이전 시대에서는 측정 장비의 한계로 극저온에서의 열용량을 측정하지 못했음), 온도에 대한 선형항이 존재합니다! 이것은 전자에 기여로 인해 발생하는 항으로, Debye model에서는 설명할 수 없습니다.
'물리학 > 고체물리학' 카테고리의 다른 글
| 6. 고체를 붙들고 있는 것: 화학 결합(What holds Solids Together: Chemical Bonding) (1) | 2024.12.02 |
|---|---|
| 5. 주기율표(Periodic Table) (0) | 2024.12.02 |
| 4. 금속 안의 전자 심화: 좀머펠트 이론(More Electrons in Metal: Sommerfeld Theory) (0) | 2024.12.02 |
| 3. 금속 안의 전자: 드루드 이론(Electrons in Metal: Drude Theory) (0) | 2024.12.02 |
| 1. Introduction (0) | 2024.12.02 |
