
이전 장에서 드루드 모델(Drude model)을 이용하여 고체의 열용량을 해석하기 위한 노력을 했습니다. 그러나 마지막 즈음에 실제로는 극저온에서 온도에 선형적으로 비례하는 열용량 항이 존재함을 보였었고, 따라서 드루드 모델이 실패했음을 알게 되었습니다. 하지만 이 선형항 역시도 설명하기 위해 노력한 물리학자가 있습니다. 바로 독일의 이론물리학자 아놀드 좀머펠트(Arnold Sommerfeld)입니다. 오늘은 그의 이론인 Sommerfeld Theory에 대해서 알아보도록 합니다.
1) 기초 페르미-디랙 통계(Basic Fermi-Dirac Statistic)
먼저, 좀머펠트 이론에 대해서 다루기 전에 간단한 통계물리학 내용을 짚고 갑니다. 화학 퍼텐셜(Chemical potential)에 대해서 알아봅시다.

화학 퍼텐셜은 어떤 시스템에 입자 하나를 추가하는데 필요한 자유 에너지를 말합니다. 어렵지 않게 생각해볼 수 있습니다. 전자기학에서 전기장이 가지는 에너지를 유도하면서 가장 단순하게 시작하는 상황은, 어떤 점전하를 놔두고 그곳에 또 다른 점전하를 놓을 때입니다. 이때는 입자 하나를 추가하기 위해서 에너지가 필요하죠. 동일한 맥락으로 생각해볼 수 있습니다.
이렇게 입자 하나를 추가하는데 필요한 에너지를 나타내는 화학 퍼텐셜은, Fermi-Dirac distribution에서 나타납니다. 지수함수 위에 올라가게 되죠.

이때 Fermi-Dirac distribution은 0 K(절대영도)에서 헤비사이드 계단 함수(Heaviside step function)와 동일해집니다. 물론 실제로는 절대영도에 도달할 수 없지만, fermion들이 점유하는 형태가 이론적으로 그렇게 된다는 말입니다. 이것을 수식적으로 확인을 해봅시다. 절대영도에 도달했다고 하면 역온도(inverse temperature β)는 무한대로 발산하게 됩니다.
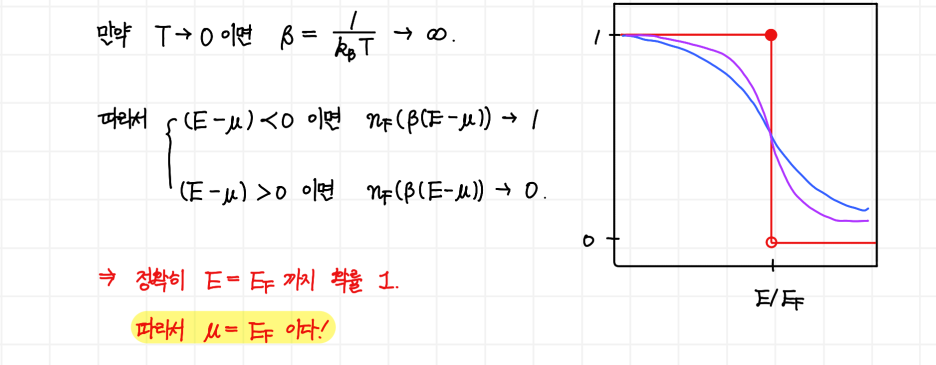
이때 두가지의 경우를 나눌 수 있는데, 괄호 내부의 값 (E-μ)가 음수라면 Fermi-Dirac distribution nF는 1이 되고, 반대로 괄호 내부의 값이 양수라면 nF는 0에 수렴하게 됩니다. 그래서 위의 그림처럼, 절대영도에서는 계단 함수의 형태를 하게 되는 것입니다. 이때 정확히 "뚝 떨어지게 되는 지점"의 에너지 값을 페르미 에너지(Fermi energy, E**F**)라고 합니다. 절대영도는 누가봐도 시스템의 모든 입자들이 가장 낮은 상태를 차지한 경우입니다. 따라서 여기서 입자 하나를 추가하게 되면, 페르미 에너지까지 꽉 차 있는 공간에 "페르미 에너지만큼의 에너지를 투입"하여야 합니다. 따라서 이것은 화학 퍼텐셜의 정의와도 일치합니다.
따라서, 페르미 에너지를 화학 퍼텐셜로써 취급합니다.
이제 아래에서 곧 fermi energy를 유도할 것입니다. 먼저 fermion의 분산 관계(dispersion relation)를 써봅니다. 파수 벡터 k와 에너지 ε 사이의 관계는 다음과 같습니다.

그리고, 열/통계물리학의 내용에 따라 우리가 전체 입자 수 N을 구하기 위해서는 아래와 같이 상태밀도함수(DOS)와 Fermi-Dirac distribution을 곱해서 모든 에너지 영역에 대해서 적분을 취해주면 됩니다. 이때 우리가 오늘 다룰 전자(electron)은 스핀 방향이 위/아래로 두 가지의 가능성을 가지므로 스핀 자유도 2를 곱해주어야 합니다.
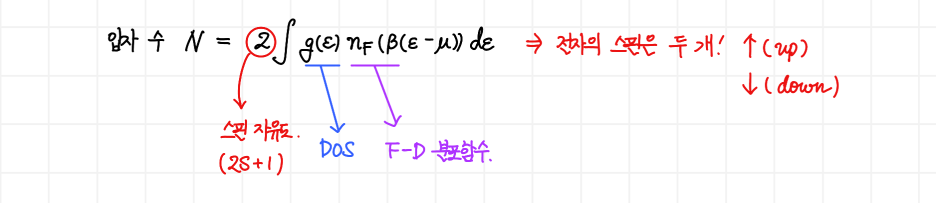
이제 절대영도를 가정하고 페르미 에너지를 구하면 됩니다만, 그전에 페르미 에너지에 대한 정의와 다양한 개념들을 정립하고 갑시다.

위에서 말했듯, 페르미 에너지 $E_F$는 T = 0 인 상태에서의 화학 퍼텐셜을 의미합니다. 이를 온도 차원으로 바꿔서 표현할 수 있는데요, 이것은 페르미 온도(Fermi temperature)라고 합니다. 똑같은 논리로 페르미 파수 벡터(Fermi wave vector) $\mathbf{k}_F$도 정의할 수 있습니다.
이렇게 구해진 개념들을 이용하면, 간단한 관계식과 물리적 정의을 이용하여 페르미 운동량(Fermi momentum)과 페르미 속도(Fermi velocity)까지도 유도할 수 있습니다.

여기서 하나 오해하고 있는 것이 있을 수 있는데, 페르미 에너지가 항상 계에서 점유된 상태 중 제일 높은 상태를 대변하지 않는다는 것입니다.

연속적인 에너지 구조에서는 페르미 에너지가 가장 높은 상태의 에너지를 말하는 것이 맞습니다만, 이산적인 에너지 구조를 가질 경우 페르미 에너지는 가장 높은 상태를 나타내지 않습니다. 예를 들면 온도가 조금이라도 높아지게 되면 입자들은 들뜨게 되며 낮은 상태인 가전자대(valence band)에서 전도대(conduction band)로 이동하게 됩니다(*추후 띠 이론-band theory-에서 더 자세하게 다룰 것입니다).
이런 경우는 Fermi energy는 가전자대와 전도대 사이의 중간에 위치하게 됩니다. 따라서 가장 높은 상태라고 말할 수는 없죠.
자, 이제 fermi energy를 계산하여 수치적으로 확인해봅시다. T = 0에서 F-D distribution function이 step function이 됨을 이용하면, 전체 입자 수에 대한 적분은

이 됩니다. 이때 저자에 따라서 상태밀도함수 g(ε)에 부피 인자 V를 포함시켜서 쓰는 경우가 있으나 제가 참고하는 서적에서는 V를 포함하지 않고 계산하므로, 저도 이 표기를 따라가도록 하겠습니다.
그러면 일반화된 DOS의 정의에 따라 g(ε)를 아래와 같이 유도할 수 있습니다.

이제 이 결과를 N에 대한 관계식에 대입하여 계산을 진행해줍시다. 이때 절대영도라는 가정 하에, 결국 F-D distribution이 step function으로 바뀌므로 적분 구간을 [0, ∞)에서 [0, εF]로 바꾸어 줄 수 있습니다.

이때 전자의 스핀 양자수 s=(1/2)를 대입하여 스핀 자유도를 2로 만들어주어 곱했습니다. 그러면

의 관계식을 얻게 됩니다. 또한 N/V는 입자 밀도 n으로 표현할 수 있습니다. 이제 양변에 (2/3) 제곱을 취해주게 되면

을 얻고, 여기서 εF에 대해서 식을 정리해주면

Fermi energy $\epslion_F$에 대한 표현을 얻을 수 있습니다. 위의 표현을 보면 알듯이, 입자 밀도 n과 입자의 질량 m을 알면 Fermi energy를 구할 수 있습니다. 위의 식을 통해서 구리(Cu)의 Fermi energy를 구해보면 약 7 eV(전자 하나가 7 V의 전위차를 느낄 때의 에너지)를 얻습니다. 이것을 온도 단위로 변환하면 약 80000 K의 페르미 온도를 얻습니다! 실온에 비해서 매우 높은 온도입니다!
이것은 금속 내의 전자들이 매우 빠른 속도를 가진다는 것을 보여줍니다!

이것은 굉장히 놀라운 결과입니다. 실제로 대부분의 금속들은 80000 K의 온도에 도달하기 한참 전에 상변화를 일으킵니다. 그럼에도 불구하고 전자들이 이렇게 높은 에너지를 갖는 것은 파울리 배타 원리(Pauli-exclusive principle)에 의한 것입니다. 전자의 밀도가 높으면 파울리 배타원리에 따라 그 밀집도만큼 강력한 척력을 느끼게 됩니다. 따라서 전자 밀도가 높으면 속도가 빨라지게 됩니다.
2) 전자의 열용량(Electronic heat capacity)
이제 전자의 열용량을 구해볼 차례입니다. 간단한 통계역학적 지식을 이용하면 전자 시스템의 에너지 E는 다음과 같이

의 적분을 수행하여 구할 수 있고, 입자 수 N에 대해서는 다음과 같은 적분

을 통해 구할 수 있었습니다. 이 적분식이 조금 복잡해보인다면, 위에서 구한 fermi energy에 대한 표현을 도입하여 더 깔끔하게 정리할 수 있습니다.

$\frac{2m}{ħ^2}^{3/2}$의 표현이 fermi energy로써 위와 같이 표현됨을 이용하면, DOS의 표현에 그대로 끼워넣어서

로 나타낼 수 있습니다. 여기서 명백하게 확인할 수 있는 것은, 상태밀도함수 g(ε)는 단위 부피 당 상태밀도의 차원을 가진다는 것입니다.
이제 total energy를 구했으므로, 이것을 온도에 대해 미분해주어 전자의 열용량 $C_{el}$을 구할 수 있습니다.

그러나, 함수가 너무 복잡하기 때문에 해석적으로 적분을 취할 수가 없습니다! 그래서 우리는 약간의 근사를 통해서 적분을 간단하게 만들 것입니다. 아까 Fermi temperature가 굉장히 높았다는 것을 잘 떠올려 보면, 우리는 실제 온도가 페르미 온도보다 훨씬 낮다고 가정을 할 수 있습니다. 이런 경우 절대영도에서의 분포함수인 step function에 비해 크게 바뀌지 않는다고 생각할 수 있죠.

따라서 화학 퍼텐셜 μ값이 EF와 크게 달라지지 않는다고 가정합니다. 이렇게 가정을 세워놓고 계산을 진행해봅시다. 먼저 F-D distribution의 특성을 이용해 아래와 같은 등식을 세워봅시다.

여기서 좌측은 임의의 온도에 대한 입자 수 적분을 의미하고, 우측은 절대영도에서의 입자 수 적분을 의미합니다. 우리가 새로이 입자를 투입하지 않는 한, 이 등식은 항상 성립하여야 합니다.
여기서 좌변의 항에 대해 적분 구간을 쪼갤 것입니다. 이때 쪼개는 기준값은 페르미 에너지 εF 입니다.

이제 같은 적분 구간을 가진 항끼리 묶어줍니다. 그러면

을 얻습니다. 좌변이 0입니다. 즉, 이 식을 더한다고 하더라도 아무런 영향을 주지 않는 것입니다. 이 식을 1번 식이라고 칭하겠습니다.
그리고, 온도가 약간 상승했다고 가정합니다. 그러면 페르미 에너지보다 높은 에너지를 갖는 "들뜬 상태"에 존재하는 입자들이 가지는 에너지와, 페르미 에너지보다 낮은 에너지를 갖는 "빈 상태"를 고려할 수 있습니다. 낮은 상태에 있던 전자가 외부의 열에너지로 인해 들떴다고 생각하는 것입니다. 이때 들뜸으로 인한 에너지 차이를 ΔE라고 합시다.

위의 그림을 보면 더욱 편하게 이해할 수 있습니다. 이 그래프는 DOS와 F-D distribution이 곱해진 함수를 에너지에 대해 나타낸 것입니다. 초록색의 "빈 상태"를 점유하던 입자들이, 들뜸으로써 푸른색의 "채워진 상태"쪽으로 옮겨간 상황입니다.
이 경우는 에너지를 구하고 있으므로, 이전에 이용하던 피적분 함수에 에너지 ε를 곱해주면 전체 에너지를 구할 수 있습니다! 따라서 아래처럼 식을 세웁니다.

이 식을 2번 식이라고 칭하겠습니다. 그러면 이제 1번 식과 2번 식을 더해보도록 하겠습니다.

그러면 위의 결과를 얻습니다. 여기서 약간의 물리적인 해석을 하자면, 우변의 제1항은 페르미 에너지 εF보다 높은 상태에 있는 입자들의 에너지를 말하고, 제2항은 페르미 에너지보다 낮은 상태에 있던 입자들의 에너지를 말합니다. 즉 우리는 적절하게 전자가 관여하는 에너지 차이를 구했습니다. 에너지를 투입함으로써 전자가 들뜨게 되었고, 이것은 고체의 열용량에 미묘하게 영향을 미치게 될 것을 암시합니다(꾸준히 언급했떤 고체의 선형적인 열용량에 대해).
이제 열용량을 구하기 위해서는 위의 값을 온도에 대해 미분해주면 됩니다. 이때 화학 퍼텐셜은 온도에 의존하게 되는 함수이나(다른 입자들이 들뜨게 되므로), k**B**T가 매우 작아서 0.01 이하의 범위라고 가정하면(실온에서의 열에너지에 해당) 간단하게 절대영도에서의 화학 퍼텐셜인 페르미 에너지를 크게 벗어나지 않는다고 생각할 수 있습니다.

그러면 온도 의존성을 갖는 값은 오로지 Fermi-Dirac distribution n**F**(ε)이므로 이것에 대한 미분만 취해주면 쉽게 계산을 할 수 있습니다. 이때 미분을 취해주면 아래와 같이 정리가 되고

여기서 DOS에 의한 대부분의 적분 기여는 페르미 에너지 근처에서 발생하고, 나머지 영역에서는 무시할 정도로 작으므로 g(ε)에 대한 적분을 고려하지 않습니다. 상수 취급하여 g(εF)로 변환하여 적분 기호 밖으로 꺼내줍니다.
이제 미분을 취해주면 되는데, 그냥 바로 온도 T에 대해서 미분을 하기엔 꽤 복잡합니다. 따라서 chain rule(사슬 법칙)을 이용하여 쉽게 정리해볼건데요.
Fermi-Dirac distribution은 역온도 β로 기술되므로 우리는 distribution function을 β로 미분해줍시다. 그리고 chain rule을 적용하여 다시 (dβ/dT)를 곱해주면 우리가 원하는 결과를 얻을 수 있습니다.

와 같이 미분 값을 구할 수 있고, 이것을 다시 적분 기호 내의 (dnF/dT)에 대입해주게 되면,

을 얻습니다. 이 적분은 복잡해보이지만 아래와 같이 치환을 해주면


을 얻습니다. 이때 큰 음수에 대해서 적분 기여도가 작으므로 적분 하한을 음의 무한대로 근사를 할 수 있습니다. 이때 형광펜으로 칠해진 적분은 꽤 복잡한 적분 중 하나입니다. 적분표를 보고 계산하면

을 얻습니다(이 적분에 대한 계산은 나중에 다른 포스트에서 다루도록 하겠습니다).
이제 힘든 계산들이 모두 끝났습니다. 적분 결과를 정리해서, 전자의 열용량 Cel을 구하면 다음과 같습니다.

우리가 실험적인 결과로써 배웠던 선형적인 열용량을 얻을 수 있습니다! 따라서 고체에서 나타났던 열용량은 다음과 같이 그 origin을 나타낼 수 있습니다.

선형적인 항은 전자(electron)에서 기인, 세제곱에 비례한 항은 포논(phonon)에서 기인하는 열용량입니다. 또한, 페르미 온도로 나타낸 전자의 열용량을 보았을 때, 괄호 앞 항은 Drude가 가정했던 이상 기체의 열용량과 거의 같고, 괄호 내부의 항은 (1/TF)의 factor가 곱해짐으로써 실질적으로 Drude가 예측했던 전자의 열용량보다 약 100배 이상 작게 측정됩니다! 우리는 Drude model이 해결하지 못했던 과도하게 큰 열용량을 이렇게 해결할 수 있었습니다.

그리고 이것은 Drude model의 또 다른 취약점 중 하나인 Peltier coefficient와 Seebeck coefficient를 실제 값과 유사하게 맞출 수 있는 결과를 줍니다!
하지만, Sommerfeld theory 역시도 완벽한 것은 아닙니다. 자유 전자 이론을 통하여 구해진 저온에서의 금속 열용량 중, 실제 값과 크게 차이가 나는 경우가 있습니다. 그 외에도 다양한 문제들이 있는데, 이것은 결론적으로 물질 내의 원자의 주기적인 구조가 고려되지 않았다는 것입니다. 이것은 지속적으로 언급하는 띠 구조(Band structure)에서 알아보도록 하겠습니다.
'물리학 > 고체물리학' 카테고리의 다른 글
| 6. 고체를 붙들고 있는 것: 화학 결합(What holds Solids Together: Chemical Bonding) (1) | 2024.12.02 |
|---|---|
| 5. 주기율표(Periodic Table) (0) | 2024.12.02 |
| 3. 금속 안의 전자: 드루드 이론(Electrons in Metal: Drude Theory) (0) | 2024.12.02 |
| 2. 고체의 비열(Specific Heat of Solid) (1) | 2024.12.02 |
| 1. Introduction (0) | 2024.12.02 |