
7장을 생략(추후 작성), 바로 9장으로 넘어왔습니다. 8장은 포스트를 쓰고 싶은데 사실 이미 열및통계물리학 포스트에서 언급한 내용이 있어서 작성할지 고민을 좀 해봐야 할 것 같아요. 애초에 6/7/8장이 짧아서 굳이 어려운 내용들을 설명하지 않아도 되지만, 그래도 글을 쓰는 사람 입장으로서 완벽하면 기분이 좋거든요.
오늘 언급할 내용은 포논(Phonon)을 도입하기 위한 기초를 언급한다고 보시면 됩니다. 먼저 첫번째 순서로는 고전역학적인 방법을 통해 진동(vibration)을 설명할 것이고, 두번째 순서로 양자역학적인 방법을 통해서 살펴보도록 할 것입니다.
Preface
가장 먼저, 질량이 m인 원자들이 일렬로 배치되어 있고 그 사이에 스프링이 있다고 생각합시다. 이 원자들 사이의 평형 거리(equilibrium length)는 a라고 합시다.

그리고 각 원자들의 위치를 xn, 그리고 그 원자들의 평형점을 xn0라고 하겠습니다. 그러면 가장 왼쪽의 원자부터 시작해서, n번째 원자의 평형점인 xn0은 na로 표기할 수 있습니다.
따라서, 평형점을 벗어난 경우에서 이동한 변위(displacement)는 다음과 같이 표현할 수 있습니다.

우리는 용수철 형태의 복원력을 가정하였기 때문에, 원자 사이가 멀어지면 가까워지는 방향으로 힘이 작용하고, 사이가 가까워지면 멀어지는 방향으로 힘이 작용합니다. 온도가 매우 높지 않다면, 이러한 복원력에 대한 potential을 2차 함수로 근사(조화 근사, harmonic approximation)할 수 있습니다. 따라서 우리는 potential을 다루기 쉬운 형태인 2차 함수(quadratic)으로 가정하겠습니다.
그러면 원자 간 총 퍼텐셜 Vtot는 다음과 같이 표기할 수 있습니다.

여기서 xi+1-xi-a는 (i+1)번째 입자와 i번째 입자 사이의 거리에서 평형 거리인 a를 뺀, 즉 평형점(equilibrium point)로부터의 변위를 나타냅니다. 2차 함수 퍼텐셜을 가정하였으므로, 우리는 이것의 제곱에 비례하는 퍼텐셜로 식을 나타낼 수 있습니다.
이 식을 각 순서의 입자에 대해서 조금 더 자세히 전개하면, 아래와 같이 쓸 수 있습니다.

그리고 아까 위에서 정의했던 displacement 형태의 δ로 나타내면 마지막 식이 됩니다.
이제 우리는 고전역학을 적용하기 위해서 힘(force)을 구할 것입니다. 힘은, 퍼텐셜의 음의 미분으로 정의됩니다. 따라서

로 미분을 취할 수 있습니다. 이때 우리는 총 퍼텐셜 Vtot에 대해서 그 표현을 구하였고, 따라서 n번째 입자에 작용하는 힘을 구하기 위해서는 x**n**으로 편미분을 취해주어야 합니다. 그러면 Summation의 정의와 편미분에 의해 딱 두 가지 항에만 미분이 작용됩니다. 바로 (δxn+1-δxn)2과 (δxn-δxn-1)2 항입니다. n번째 원자의 위치 xn에 대한 항을 포함하고 있는 것이 바로 이 두 개이기 때문이죠. 그러면 식을 전개해볼까요?

위와 같은 결과를 얻습니다. 그럼 우리는 힘을 구했으므로 이제 운동 방정식을 풀 차례입니다. 좌변을 F=ma 꼴로 표현합시다. 그러면

의 방정식을 만족하는 δxn을 찾아야 하는 문제로 귀결됩니다. 우리는 해를 완벽하게 알 수 없지만 이러한 시간에 대한 상수 계수 2계 미분 방정식을 푸는 방법을 대략적으로 알고 있습니다. 바로 Aexp[i(ωt-kx)] 형태의 해를 가정하는 것입니다.

이것을 대입하여 k에 대한 조건을 얻어봅시다.

대입 후 우변을 전개합니다. 그리고 동류항 κAei(ωt-kna)로 묶어주게 되면 마지막 식의 형태로 정리되는데요. 좌우변에 동일한 exp 항이 있으므로 나누어줍니다. 그러면

을 얻고, (1-cos(ka))를 반각 공식을 이용해 sin2(ka/2) 형태로 나타낼 수 있습니다. 양변에 제곱이 있으니 쉽게 정리해줄 수 있겠내요. 따라서 각진동수는

을 얻습니다. 이것을 정규 모드 진동수(Normal mode frequency)라고 합니다. 이 정규 모드 진동수는, 모든 입자가 같은 진동수로 가진다고 가정했을 때의 값입니다.
이때 sine function은 주기성을 가지는, 주기 함수입니다. 이때 k를 변수로 생각했을 때 주기는 (1/2)×(4π/a)=(2π/a) [sine function에 절댓값이 취해져 있으므로 주기에 1/2을 곱했습니다]를 갖습니다.
이것을 ω vs k의 그래프로 나타내게 되면, 다음과 같습니다.
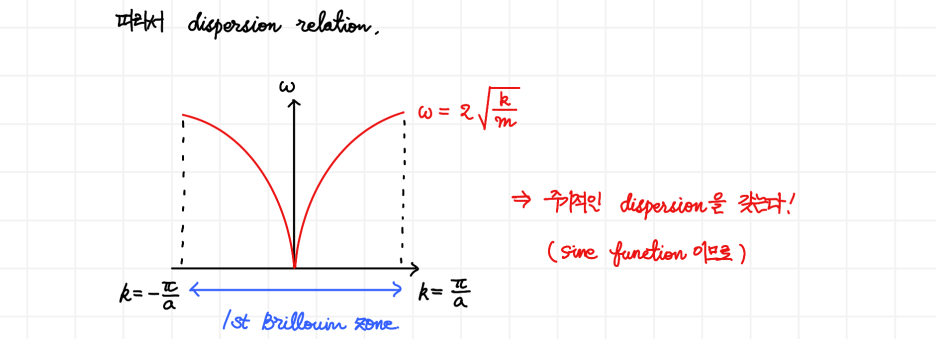
이 그림에서는 [-(π/a), (π/a)]에 대한 영역만 표현을 했지만, k가 더 작아지거나 커지도라도 주기적인 진동을 반복합니다. 즉, 주기적인 분산 관계(periodic dispersion relation)를 갖는다는 것입니다! 따라서 모든 영역에 대해서 표현하지 않고 가장 작은 단위 주기에 해당하는 영역에 대해서만 그림을 그렸습니다. 추후에 설명하겠지만, 이 영역을 '첫번째 브릴루앙 영역(1st Brillouin zone)'이라고 합니다.
1) 역격자에 대한 첫번째 대면(1st exposure to the reciprocal lattice)
위의 분산 관계식을 조금 더 자세히 설명해보도록 하겠습니다. 위에서의 분산 관계식은, k 값이 k+(2πn/a) (여기서 n은 정수-integer)가 되어도 동일한 각진동수 ω값을 가지는 것을 보여줍니다.

여기서 k 공간을 역격자 공간(reciprocla space)이라고 합니다. 우리가 처음에 용수철 사슬 모형을 가정하였을 때는, 격자가 x → x+a의 주기성을 갖는다고 가정했습니다. 즉, 실공간에서는 a만큼의 주기를 갖고, 이것이 역공간으로 projection되면 (2π/a)의 주기를 갖게됩니다.
따라서, 우리는 앞으로 자주 사용하게 될 이 개념에 대해서 새로운 정리를 하나 만들 수 있습니다.

그렇다면 왜 주기적으로 나타나는 것일까요? 우리가 가정한 시험 해(trial solution) δxn의 정의를 다시 한 번 살펴봅시다.
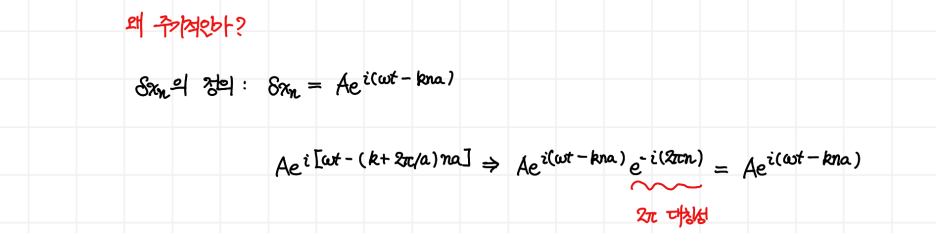
여기서 지수 항의 k 값을 k+(2π/a) 치환해서 다시 식을 전개하면, 위의 전개식과 같이 e-i(2πn)이 튀어나오게 됩니다. 이때 n이 정수라고 생각하면 이 값은 항상 1을 줍니다.

이는 곱셈의 항등원이죠! 따라서 값이 바뀌지 않고 동일한 결과를 주게 됩니다. 즉, 우리는 k에 대해 (2πn/a)의 주기를 가진 모든 점**들은 물리적으로(=수학적으로) 동등한 결과를 준다고 말할 수 있는 것입니다!** 이때 이 점들의 집합을 역격자(reciprocal lattice)라고 합니다.
실공간의 격자 x=na와 비교하여 역격자와 구별할 필요가 있기 때문에, 실공간의 격자는 실격자(direct lattice) 혹은 실공간 격자(real space lattice)라고 부릅니다.

위에서도 언급했듯, a(격자 상수, lattice constant)에 대해 역수가 취해지고 2π가 곱해진 공간을 역공간(reciprocal space, 이것이 곧 k space)이라고 하고, 이러한 k space에서의 단위 셀(unit cell)을 브릴루앙 영역(Brillouin zone)이라고 합니다.

여기서 특히나 특별하게 다루는 녀석이 하나 있는데, 아까 dispersion relation의 그래프를 그릴 때 언급했떤 1st Brillouin zone입니다. 이것은 k=0 값을 기준으로 한, k space에서의 단위 셀을 의미합니다.
그러면 2nd, 3rd ... 등의 Brillouin zone들을 언급할 수 있는데요, 이러한 zone들의 경계선을 zone boundary(영역 경계)라고 합니다. 이러한 zone boundary는 k=±(nπ/a)에서 나타납니다.

앞에서부터 k space의 주기에 대한 언급을 꾸준히 했습니다. 우리는 이것을 Gm이라는 문자를 도입하여 이 주기를 정의할 수 있습니다.

그러면 한껏 보기가 편해집니다. xn과 Gn의 값을 비교하여 볼까요?
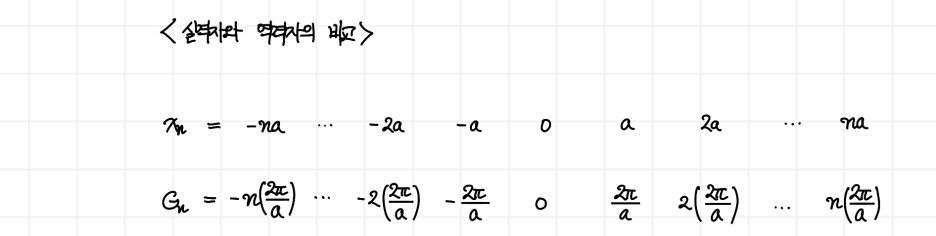
이 결과는, xn과 Gn의 곱이 다음과 같이 나타남을 예측할 수 있게 해줍니다.

그런데 무심코 넘어가버렸지만 약간의 의문점이 있습니다. 우리가 일반적으로 알기로는, 파장이 짧은(진동수가 큰) 파동일수록 더 큰 에너지를 갖는다고 알고 있습니다.

그러면 파장의 역수인 k 값이 다르다는 것은, 곧 서로 다른 파동을 준다는 것 아닌가요? 어떻게 동일하게 주기적이라고 취급할 수 있는거죠?
이 문제의 정답은 바로 떠오르지 않을 수도 있습니다. 이것은 우리가 연속적인 파동을 다루는 것 같은 착각을 갖고 있기 때문입니다.
실제로 real space와 k space는 이산적인(discrete) 격자점을 갖습니다. 이 소리는, 파동이 모든 격자점에서 정의되는 것이 아니라는 것이죠.

우리가 주기성을 갖는다고 말했던 경우는, 오직 x**n**=na인 지점에 대해서만 동등하다고 말하는 것입니다(불연속적이라는 것이죠). 결국 우리가 보고자 하는 것은 각 격자점들의 진동을 거시적으로 파동으로 해석하는 것입니다. 하지만 그 파동이 미소 길이에 대해서 존재하는 것이 아니라, 제일 작은 어떤 값을 기준으로 더 이상 파동을 쪼갤 수가 없게 됩니다. 파동이라는 것은 결국 원자들이 진동하는 것이므로, 원자 사이의 거리에서도 진동한다고 말할 수 없을테니까요.
아래의 그림을 보면서 더욱 쉽게 이해해봅시다.
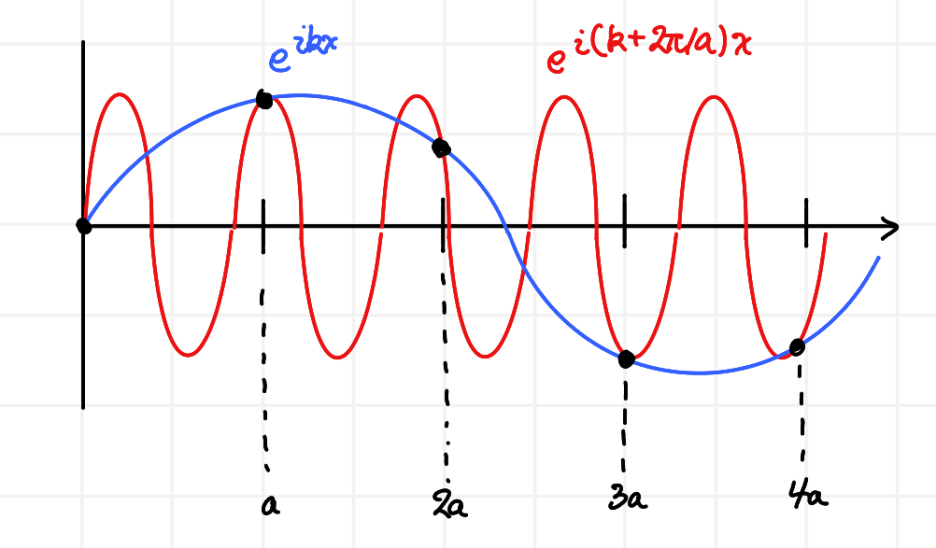
위의 그림을 보면, 서로 다른 두 파동이 특정한 점 xn=na에서 만나는 것을 볼 수 있습니다. 그래프를 자세히 보면 그 사이에서도 만나긴 합니다만, 실제로 정의되는 것은 아닙니다. 애초에 원자가 0, a, 2a, 3a, ...의 평형점에만 배치되어 있으니까요. 결국 두 파동이 만나는 지점은 오직 na 꼴의 위치에만 정의된다는 것입니다.

다른 점에서는 일치하지 않구요. 애초에 우리가 파동으로 판단하기 위한 데이터 자체가 없다고 보시면 됩니다. 그러면 우리가 파동으로 인지할 수 있는, 원자들의 진동에 대한 최소 간격은 a입니다. 이 점만을 바라보고 k와 k+(2π/a) 값을 갖는 두 파동을 바라보면, 우리는 그 둘을 구분할 수 없습니다.

이렇게 우리가 샘플링할 위치가 이산적이어서 두 파동이 동일하게 보이는 것을 파동의 앨리어싱(aliasing)이라고 합니다.
2) 1차원 사슬의 분산 특성(Properties of the dispersion of the one-dimensional chain)
이제 1차원 사슬에 대한 기초적인 논의가 어느정도 끝났습니다. 그러면 k 값이 변함에 따라 어떠한 분산 특성을 가지는 알아봅시다.
먼저, 음파와 포논이 관련이 있다는 사실을 대충은 알고 계실 겁니다. phonon의 어원 자체가 음악, 음향이라는 개념에서 튀어나왔으니까요. 원자/분자들의 진동이 결국 소리를 나타냅니다.
이때 우리가 원자 크기와 비교를 해보면, 소리(음파)의 파장은 굉장히 큰 값을 갖습니다! 즉, 장파장이라는 소리죠. 그러면 장파장 극한에 대해서 논의를 해봅시다.

파장이 무한대인 경우, 파장의 역수인 k 값은 반대로 0에 수렴하게 됩니다.
장파장 극한(Long wavelength limit)
음파의 속도는 분산 관계로써 정의됩니다. 각진동수 ω를 파수벡터 k로 나누어주게 되면 음파의 속도 vsound를 얻게 됩니다. 여기서 일차원 사슬의 각진동수(위에서 구한)를 다시 가지고 오면
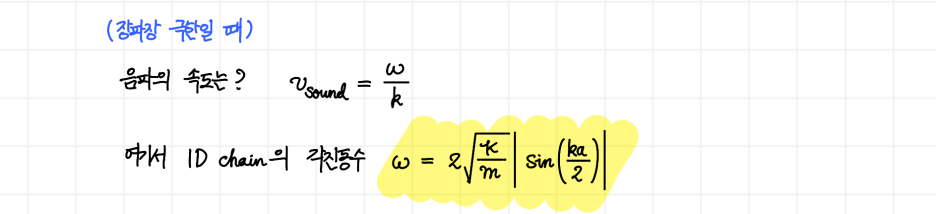
입니다. 여기서 k를 0으로 보내봅시다. 이때 마구잡이로 0을 대입하면 안되고, Taylor expansion을 취하여 그 값을 근사해줄 것입니다.

Taylor expansion을 통해, 작은 x 값을 가정하고 1st dominant term까지만 취해주면 sin(ka/2)≒(ka/2)를 얻을 수 있습니다. 따라서 각진동수는 아래와 같이 바뀌게 됩니다.

그리고 이 표현에서 양변을 k로 나누어주면 음파의 속도를 계산할 수 있죠.

이렇게 계산된 값은 선형 분산 관계에 따라 음파의 속도가 상수로 나타나게 됩니다. 그러나, 단파장인 경우(큰 k 값에 대하여) 이러한 분산 관계는 깨지게 됩니다. 아래에서 그 경우에 대해서 논의해봅시다.
단파장(Short wavelength)
단파장인 경우, 위의 경우처럼 하나의 속도만을 고려할 수는 없습니다. 군 속도(group velocity)와 위상 속도(phase velocity)를 동시에 논의합시다.
먼저 군 속도는, 파동묶음(wave packet) 자체가 움직이는 속도를 말합니다(쉽게 말해 envelope가 움직이는 속도입니다).

이는 각진동수를 파수벡터 k로 미분한 값으로 정의됩니다.
둘째로 위상 속도(phase velocity)는, 각 소규모 파동의 최댓값(Maximum value)과 최솟값(Minimum value) 자체가 envelope 안에서 이동하는 속도를 말합니다. 이것이 아까 장파장의 경우에서 정의했던 속도와 동일합니다.

각진동수를 파수벡터로 나누어주면 구할 수 있습니다.
이렇게 단파장의 경우는, k→0의 근사를 취할 수 없으므로, 정직하게 미분과 나눗셈을 취해주어야 합니다. 그러면

의 결과를 얻습니다. 군 속도의 경우 미분하여 cos 형태가 되고, 위상 속도의 경우 sinc function을 얻게 됩니다.
여기서 두 가지 성질을 유도할 수 있습니다. 만약, k→0(장파장 극한)이라면 군 속도 v**g와 위상 속도 vp**는 동일합니다. 또한 k가 zone boundary 값을 가지게 된다면 군 속도 v**g**는 0이 됩니다.
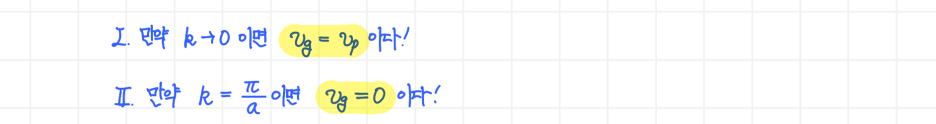
한 번 대입함으로써 두번째 성질을 증명해볼까요? 우리가 시험 해로 잡았던 지수 함수의 k 값에, zone boundary의 조건인 k = (π/a)를 대입해봅시다.

그러면 n이 정수라는 가정에 따라 양의 계수를 가진 파동과 음의 계수를 가진 파동이 둘 다 가능한 해를 준다는 것을 알 수 있습니다. 이렇게 위상이 서로 반대인 파동이 만나서 중첩(superposition)되면 어떻게 될까요? 바로 정상파(standing wave)를 형성하게 됩니다. 정상파는 envelope이 정지한, 깔끔한 파동이죠. 따라서 군 속도가 0이 되는 것이죠.
정규 모드의 셈(counting normal mode)
우리는 분산 관계에 따라, k 값이 정해져 있음을 알고 있습니다.

그렇다면 특정 k 값을 갖는 정규모드는 총 몇개가 있을까요? 이것을 구하기 위해 주기 경계 조건 혹은 보른 본 카르만 경계 조건(periodic boundary condition or Born-von Karman boundary condition)을 적용합니다. 그러면 아래와 같은 관계식을 얻을 수 있습니다(위에서 했던 과정과 동일하므로 자세한 설명을 생략합니다).

여기서 p는 임의의 정수입니다. 그리고 N은 총 입자수로, 격자 상수 a와 곱했을 때 사슬의 총 길이 L을 얻게 됩니다.
그러면 우리는 k 값의 간격과, k 값을 가질 수 있는 범위를 지정할 수 있습니다. 그리고 우리가 현재 구하고자 하는 값은 "가능한 k 값의 수"이므로, k가 정의된 영역을 단위 길이(간격)으로 나누어 주면 그 수를 구할 수 있겠네요.

그렇게 그 값을 구해보면, N을 얻습니다! 즉, 1차원 사슬의 정규 모드는 입자 수 N만큼 존재한다는 것이죠. 즉 원자 당 하나의 정규 모드를 가지게 됩니다. 이것이 바로 Debye가 발산하는 적분을 cutoff 하기 위해 예측했던 결과랍니다!
3) 양자 모드: 포논(Quantum Modes: Phonon)
이제 포논에 대해서 배워볼 차례입니다. 양자역학과 고전역학은 서로 다른 결과를 주는 것 같지만, 사실은 그렇지 않습니다. 미시 세계에서 양자역학이 적용될 때, 그것을 거시 세계에서의 컨디션으로 근사하게 되면 고전역학이 되는거죠. 이것을 대응 원리(quantum correspondence principle)이라고 합니다.

대응 원리는, 양자 상태를 기술하는 양자수가 매우 커지게 되면 그 계는 고전역학적으로 기술할 수 있다는 것을 나타내는 원리입니다.
단일입자의 1차원 양자 조화 진동자(harmonic oscillator)를 생각해봅시다. 이 조화 진동자의 에너지는 다음과 같이 나타납니다.

이것은 주어진 각진동수 ω 혹은 k 벡터에 대해 많은 고유상태(eigenstate)를 가질 수 있다는 것을 보여줍니다. 에너지를 얻고 잃음에 따라 eigenstate들을 오르거나, 내려갈 수 있습니다.

여기서 n이 매우 크면, 높은 에너지 상태를 갖게 되죠. 이것은 고전적으로 큰 진폭을 갖는 진동에 해당합니다.
여기서, 'harmonic oscillator의 상태를 하나씩 올라갈 때마다 생기는 normal mode의 들뜸'을 포논(phonon)이라고 합니다.

즉, Phonon은 진동(vibration)의 불연속적인 양자를 말합니다.

더 이해하기 쉽게 말하자면, 진동 에너지의 가장 작은 단위를 양자로써 취급하는 것으로 말할 수 있겠죠. 따라서 phonon을 입자로 해석하거나 양자화 된 파동처럼 해석할 수 있다는 것입니다.

이때, 우리가 이전의 결과에서 구했던 것처럼, 서로 다른 phonon에 대해 같은 모드(즉 같은 k 값)를 가질 수 있다는 것을 알고 있습니다. 이것은 Boson의 특징입니다. Fermion이라면 같은 상태를 가질 수 없으므로 이러한 결과를 만족할 수 없습니다.
그러면 이제 mode 수를 구할 필요가 있겠습니다. 이것은 Bose-Einstein factor n**B**(βħω)로 구해집니다.
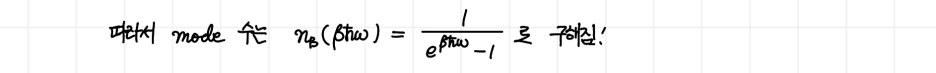
여기다가 Density of States function인 g(ω)를 곱하여 전체 구간에 대해 적분을 취해주면 모드 수 N을 얻을 수 있을 것입니다.
그리고 1차원 harmonic oscillator에서, 단일 k값에 대한 특정 상태의 에너지는 다음과 같습니다.
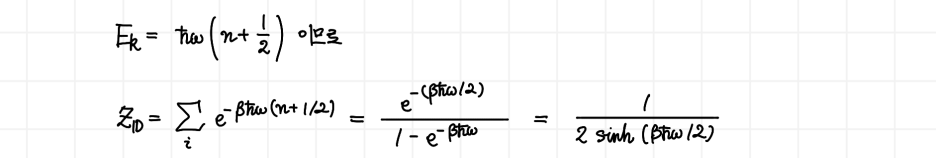
이것을 모든 n에 대해 합으로 취해주게 되면, 무한등비급수가 되어 결과를 위와 같이 정리할 수 있습니다. 분배함수의 결과를 얻은 셈이죠. 이제 분배함수를 통해 평균 에너지를 구해주면
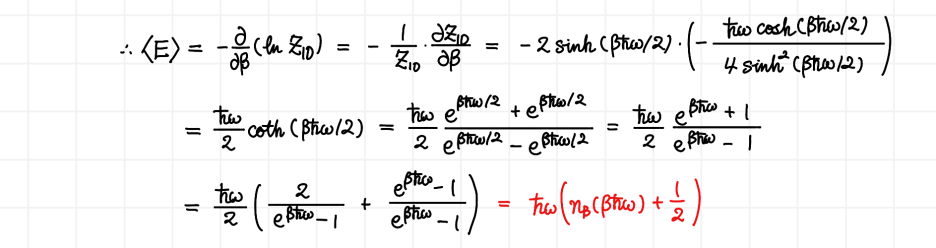
을 얻습니다. 사실 이미 2장에서 취했던 계산인데, 오랜만에 까먹을까봐 한 번 더해봤어요. 자, 그러면 이제 모든 k 값에 대한 합을 취해주면 전체 에너지 Utotal을 구할 수 있습니다.

이때 사실은 k에 대한 이산적인 합이지만, k값이 매우 조밀하게 분포한다면 이것을 적분으로 근사할 수 있습니다.

즉 연속처럼 취급하겠다는 것입니다. 따라서 Utotal은 다음과 같은 적분을 통해 구해집니다.

이때 적분 변수를 dω로 치환하게 되면, g(ω)가 factor로 나오게 됩니다. ω에 대해서 적분을 취하려면 위와 같은 형태로 적분을 해주시면 됩니다. 그러면 이 결과를 토대로 고체의 열용량까지도 구할 수 있겠죠.
지금까지 배웠던 Einstein, Debye, Toy model을 통해서 Dispersion relation을 다시 상기해보자면 다음과 같습니다.

4) 결정 운동량(Crystal Momentum)
운동량 보존 법칙(Law of conservation of momentum)을 한 번 떠올려봅시다.

운동량 보존 법칙은 일반적인 공간에서 항상 적용되는 법칙입니다. 그럼 phonon에도 이를 적용시켜도 되는 걸까요? 입자처럼 해석해도 된다고 했으니까요.
Phonon의 특성을 다시 떠올려 봅시다. 앨리어싱으로 다시 떠올려보면, 물리적으로 phonon의 momentum은 k일 때와 k+(2π/a)n일때 구분할 수 없다고 했습니다.

즉, 이것은 mod(나머지 함수) 값이 phonon에 영향을 미친다는 것을 의미합니다(a mod b는, a를 b로 나누었을 때의 나머지를 말합니다).
(2π/a)를 주기로 같은 성질을 가지므로, 임의의 k 값에 대해 k mod (2π/a)가 동일하면 같은 phonon이라고 말할 수 있는 것입니다.
여기서 결정 운동량(crystal momentum)의 개념이 등장합니다. crystal momentum은 1st Brillouin zone에서의 ħk 값을 말합니다. 이것을 위에서 이야기한 mod 함수로 다시 이야기 하자면, 결국 h(k mod (2π/a))를 말하는 것입니다. 1st Brillouin zone이 -(π/a)부터 (π/a)까지의 k space를 말하므로, 이 영역 안에 들어가는 나머지 값을 crystal momentum이라고 부르는 것입니다.

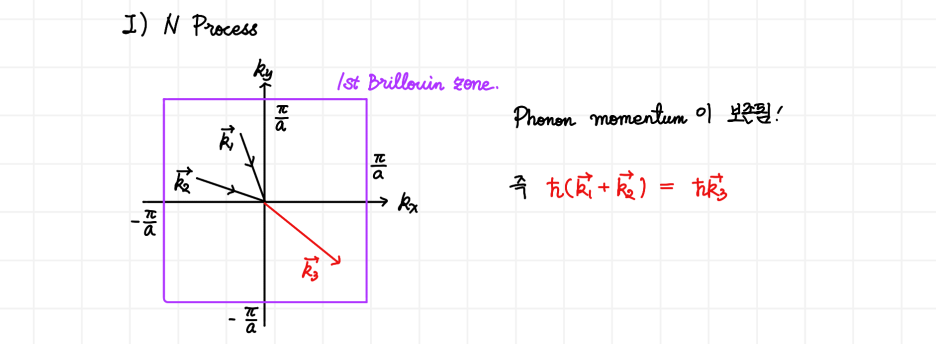
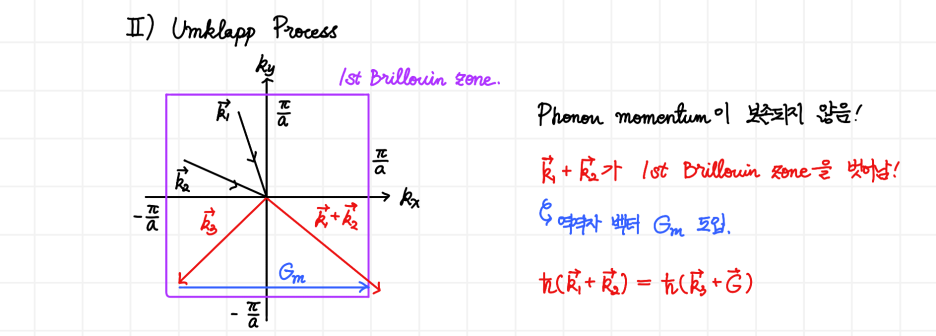
이때 phonon도 입자로 해석할 수 있다고 했으므로, phonon끼리의 충돌에서도 momentum이 보존되어야 하지만 (일반적으로) 그렇지 않고 crystal momentum 만이 보존됩니다. 실제로 이 결과는 electron-phonon, phonon-phonon interaction에 적용이 됩니다.
한번 간단 예시를 들어보죠. 특정한 결정 운동량을 가지는 3개의 phonon의 충돌을 알아봅시다.

만약 운동량처럼 생각을 했다면, 어떤 충돌을 했건 간에 결국 2πħ만큼의 운동량이 보존되는 결과를 나아야합니다. 하지만, 결정 운동량으로 생각하면

오히려 운동량을 바라보았을 때는 음의 운동량 값을 가질 수 있다는 결과를 줍니다! 즉 운동량은 보존되지 않으며, 오직 결정 운동량만이 보존됨을 알 수 있습니다. 절대적 k 값보다, k의 나머지가 중요하네요.
이러한 결과는 독일의 수학자 에미 뇌터(Emmy Noether)로부터 유도된 '뇌터의 정리(Noether's Theorem)'을 통해서 알려졌습니다. 뇌터의 정리는 "보존량은 대칭성으로부터 기인한다"는 의미를 품고 있는데요.

계가 (연속적인) 병진 대칭성을 가진다면 운동량이 보존되고, (연속적인) 회전 대칭성을 가지면 각운동량이 보존됩니다. 그리고 (연속적인) 시간 반전 대칭성을 가지면 에너지가 보존되죠.
그러나 고체 격자계에서는 연속적인 병진 대칭성을 가지지 못합니다. 원자가 띄엄띄엄 배치되어 있으므로 불연속적인 병진 대칭성을 가지게 됩니다. 이때 보존되는 물리량이 바로 결정 운동량입니다. 그래서 우리가 결정 운동량을 배우는 것입니다.
'물리학 > 고체물리학' 카테고리의 다른 글
| 11. 꽉묶음 사슬(Tight Binding Chain) (0) | 2024.12.02 |
|---|---|
| 10. 1차원 이원자 사슬의 진동(Vibrations of a One dimensional Diatomic Chain) (1) | 2024.12.02 |
| 6. 고체를 붙들고 있는 것: 화학 결합(What holds Solids Together: Chemical Bonding) (1) | 2024.12.02 |
| 5. 주기율표(Periodic Table) (0) | 2024.12.02 |
| 4. 금속 안의 전자 심화: 좀머펠트 이론(More Electrons in Metal: Sommerfeld Theory) (0) | 2024.12.02 |
