
안녕하세요, 딘입니다. 저번 포스트까지는 일차원 사슬에 대해서 알아보면서, phonon에 대한 해석을 얻을 수 있었습니다.

이번 챕터에서는, 전자에 대해서 다시 다루어보도록 할 것입니다.
1) 1차원 꽉묶음 사슬(One dimensional tight binding chain)
사실 꽉묶음 사슬(tight binding chain)에 대해서는 이미 다루었던 적이 있습니다. 6장에서 bonding에 대해서 LCAO, 혹은 tight binding theory에 대해서 언급했었는데요. 바로 그걸 본격적으로 알아보는 것입니다. 아래와 같이, a의 거리를 두고 원자들이 배열되어 있다고 생각합시다.

이때 총 N 개의 원자가 있으며, 이 원자들이 주기적으로 배열되어 Born-Von-Karman Boundary condition을 따른다고 가정하도록 하겠습니다. 즉, N 번째 원자와 1번째 원자가 연결되어 있는 것과 마찬가지입니다.
그러면 각각 임의의 i 번째 원자에 대한 파동함수를 Dirac notation으로 표기할 수 있습니다.

그리고 각 파동함수들이 서로 정규 직교(orthonormal)의 관계를 가진다고 생각해 보겠습니다. 그러면, 임의의 파동함수 Ψ는 완비성(completeness)을 보장받는다는 가정하에 각 파동함수들의 선형 결합으로 표현할 수 있습니다. 이것이 LCAO(원자 오비탈의 선형 결합) 방법입니다.

그러면 이제 Effective Schrodinger equation을 유도하도록 하겠습니다. 기본적인 Time-independent Schrodinger equation은 다음과 같습니다.

이제, 이 사이에 identity operator를 연산자와 켓 사이에 끼워넣도록 하겠습니다. 그러면

을 얻게 됩니다. 이제 직교성을 이용할 차례입니다. 현재는 identity operator를 m th state에 대해서 작용하였으므로 임의의 직교하는 다른 state인 n th state를 양변에 취해주도록 하겠습니다. 그러면 직교성에 의해

를 얻습니다. 여기서 < n | H | m >은 Hamiltonian의 Matrix element(행렬 원소)가 되어 Hnm으로 표기할 수 있습니다. 그리고 < m | φ >는 φm으로 표기하도록 하겠습니다. 그러면 Effective Schrodinger equation은 다음과 같이 정리됩니다.

이러한 방법으로 φm을 구하는 것이 우리의 최종적인 목표입니다. 하지만 여기서는 단순하게 하나의 양자수에만 의존하는 파동함수를 고려했으나, 실제로는 4개(주양자수, 궤도양자수, 자기양자수, 스핀양자수)에 의존하게 됩니다.

우리가 이렇게 많은 양자수를 고려할 수록 실제의 시스템과 유사해집니다. 하지만 단순한 시스템을 생각하여 state 당 하나의 오비탈만을 가진다고 고려해보도록 하겠습니다.
일단, Hamiltonian은 kinetic term과 potential term의 합으로 나타나게 됩니다. 이때 입자가 N개 있고 우리가 보고 싶은 m번째 전자가 느끼는 potential은, 자신이 속박되어 있는 m번째 원자핵 말고도 총 (N-1)개의 원자에 대한 Coulomb potential이 있으므로 이것 역시도 고려해주어야 합니다.

따라서, 식을 조금 더 간편하게 수정해주도록 하겠습니다. 자신이 속박되어 있는 m번째 원자에 대해서 느끼는 potential 항 Vm과, 다른 원자핵으로부터 느끼는 potential 항을 분리합니다.

그리고 이제 kinetic term과 m번째 원자핵으로부터 느끼는 potential을 묶어서 그 고유값을 ε0로 쓰도록 하겠습니다. 이제 양변에 n th state 에 해당하는 브라 벡터를 걸어주면 Effective Schrodinger equation은

을 얻습니다. 위 식에서, 우변의 2항을 양자역학에서는 교환 항(exchange term)이라고 불렀었습니다. 여기서는 조금 더 구속조건을 주어서, 이 교환 항이 발생하기 위한 조건으로 서로 맞닿아 있는 원자핵으로부터만 그 potential을 느낀다고 합시다. 즉, 두 칸 이상 떨어진 원자핵으로부터는 이러한 potential이 모두 0이라는 것입니다. 이때 이 potential의 고유값을 -t라고 하겠습니다. 이것은 깡충뛰기 항(hopping term)이라고 부릅니다(굉장히 어색하네요. 앞으로는 hopping term이라고 하겠습니다).

따라서 Hamiltonian의 Matrix element를 구하면 다음과 같습니다.

여기서 hopping이 물리적으로 의미하는 바는, 시간에 의존하는 Hamiltonian 성분으로써, transition과 관련이 되어있습니다.
자, 그러면 여기까지 우리가 풀어야 할 방정식이 정리가 된 상태입니다. 아래에서는 이 방정식의 해를 구해보도록 하겠습니다.
2) 꽉묶음 사슬의 해(solution of the tight binding chain)

우리는 현재 주기적인 퍼텐셜(periodic potential)을 가정하고 있습니다. 시험 해(ansatz)를 아래와 같이 가정해봅시다.

해를 이렇게 잡은 이유는 기본적으로 주기함수 꼴인데다, N개의 state가 있다고 가정하였을 때 그것의 normalize를 위해 계수로 나누어 준 것 입니다. 이 해를 대입해봅시다. 그러면
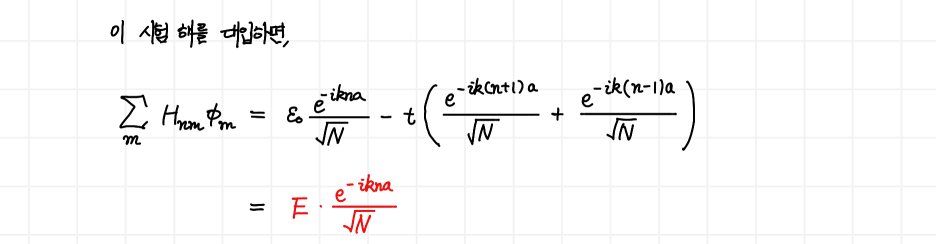
을 얻을 수가 있네요. 여기서 에너지에 해당하는 고유값을 정리해주면 다음을 얻습니다.

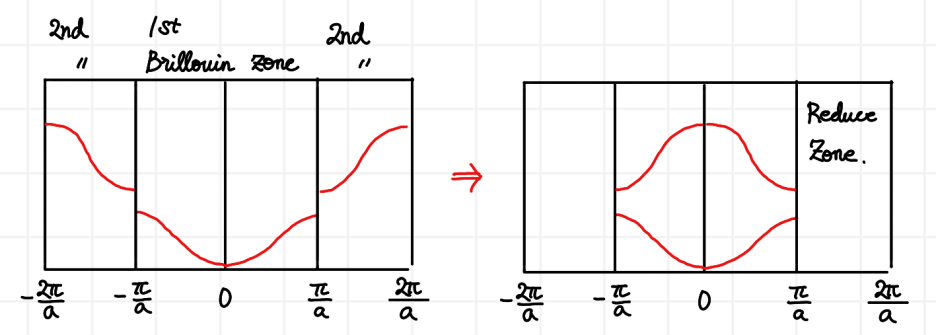
이러한 코사인 형태의 분산 관계는 우리가 지금까지 다루었던 phonon에서의 분산 관계와 매우 유사합니다. 이제 얻어진 결과를 통해 E-k diagram을 그려보도록 합시다.
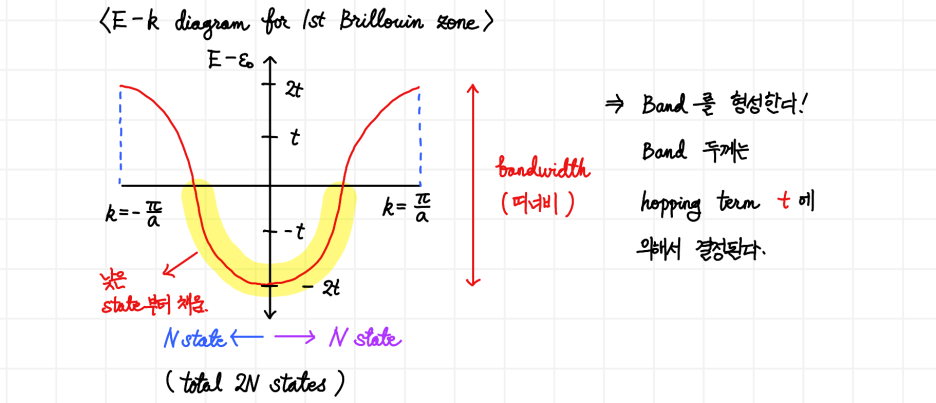
그러면 위와 같은, cosine function 형태로 진동하는 분산 관계를 얻게 되는데 이것이 전자가 가질 수 있는 상태를 의미하게 됩니다. 이때 이것이 우리가 아는 Band가 되며, 그래프의 y축을 보면 알 수 있듯 이 Band의 두께(Bandwidth)를 결정하는 것은 바로 hopping term t가 결정하는 것입니다.
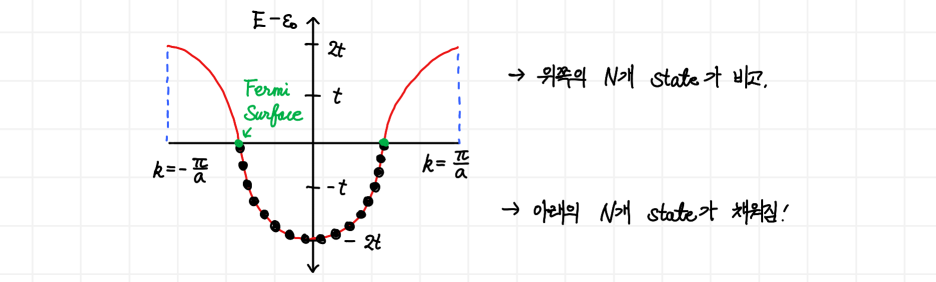
이때 Band에 존재하는 상태 수는 N*2(스핀 자유도 up/down), 즉 2N개가 되는데요. 이때 전자는 실질적으로 N개가 되므로 Band의 절반만 채우게 됩니다. 가장 낮은 에너지 상태를 말이죠.
만약, 원자가 조금 더 가까워진다면 hopping term인 t의 크기가 커지게 됩니다. 따라서 원자간 거리(interatomic distance)에 따른 에너지 그래프를 보면 다음과 같습니다.

즉, 띠의 두께(Bandwidth)가 증가하는 것을 볼 수 있습니다.
그리고 위에서 그렸던 E-k diagram에서, k=0인 지점에서 parabolic approximation을 취할 수 있습니다. cosine function을 급수 전개해보겠습니다.

여기서 2차 항만 고려하고, 그보다 높은 차수는 무시하겠습니다. 그러면 에너지 E(k)는

와 같이 표현됩니다. 이때 유효질량(effective mass)의 개념을 도입하면 k에 대한 이계도함수를 통해서 전자가 고체 내부에서 느끼는 질량을 구할 수 있습니다.
3) 띠를 채우는 전자(Electron filling into bands)


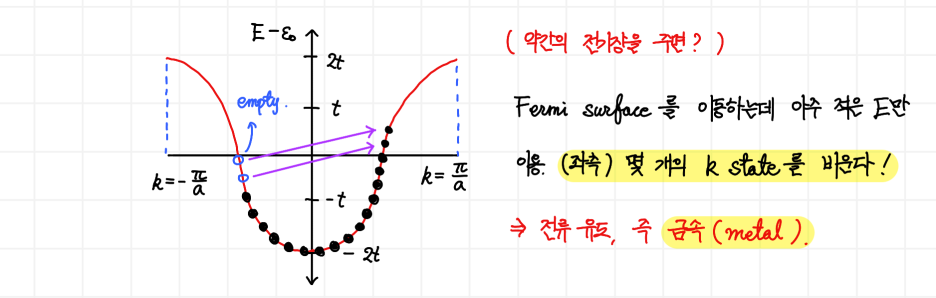


4) 다중 띠(Mulitple Bands)







'물리학 > 고체물리학' 카테고리의 다른 글
| 13. 역격자, 브릴루앙 영역, 결정 내의 파동(Reciprocal Lattice, Brillouin Zone, Waves in Crystals) (0) | 2024.12.02 |
|---|---|
| 12. 결정 구조(Crystal Structure) (0) | 2024.12.02 |
| 10. 1차원 이원자 사슬의 진동(Vibrations of a One dimensional Diatomic Chain) (1) | 2024.12.02 |
| 9. 1차원 단원자 사슬의 진동(Vibration of a One-Dimensioanl Monatomic Chain) (1) | 2024.12.02 |
| 6. 고체를 붙들고 있는 것: 화학 결합(What holds Solids Together: Chemical Bonding) (1) | 2024.12.02 |